[CVPR 2024] FreGS: 3D Gaussian Splatting with Progressive Frequency Regularization

Paper Info

• CVPR 2024
• Jiahui Zhang, Fangneng Zhan, Muyu Xu, Shijian Lu, Eric Xing
• Nanyang Technological University | Max Planck Institute for Informatics | Carnegie Mellon University | MBZUAI

 

Introduction 

 

Novel View Synthesis(NVS)는 한 장면(scene)을 여러 시점에서 촬영한 이미지를 바탕으로 장면을 정밀하게 모델링하여, 임의의 뷰포인트에서 이미지를 생성하는 것을 목표로 한다. 최근에는 NeRF를 기반으로 발전을 이루어 왔으나 긴 학습 및 렌더링 시간이 소요된다는 문제가 있다. NeRF의 유력한 대안으로 주목받는 3D Gaussian splatting(3D-GS)은 우수한 학습 및 추론 속도와 경쟁력 있는 렌더링 품질을 동시에 제공한다. 하지만 3D-GS는 가우시안 밀집화 과정에서 과잉 재구성(over-reconstruction) 문제를 종종 겪는데, 이는 고분산(high-variance) 영역이 소수의 큰 가우시안으로만 표현되어 학습된 결과물에서 결함이 생기는 상황을 의미한다. 이러한 과잉 재구성은 블러(blurring) 및 왜곡(artifacts)를 발생시킨다. 

 

본 논문은 과잉 재구성이 주파수 스펙트럼의 불일치로부터 명확히 드러난다는 점에 착안하여, 이 문제를 해결하기 위한 3D Gaussian splatting 기법인 FreGS를 제안한다. FreGS는 푸리에 공간에서의 주파수 신호를 정규화하여 과잉 재구성을 완화하는 접근법을 취하며, 이를 위해 새로운 주파수 어닐링(frequency annealing) 기법을 도입해 점진적 주파수 정규화(progressive frequency regularization)를 구현한다. 구체적으로 FreGS는 저주파 신호에서 고주파 신호로 단계적으로 정규화 범위를 넓혀가며 coarse-to-fine Gaussian densification를 수행한다. 이는 저주파 신호가 주로 전역 패턴이나 구조(대규모 특징)을, 고주파 신호가 주로 국소적인 세부(소규모 특징)를 담고 있다는 점에 근거한다. 이러한 점진적 정규화는 렌더링된 이미지와 실제 정답 사이의 주파수 스펙트럼 차이를 최소화하여, 주파수 공간에서의 정확한 지침을 제공하고 공간적 픽셀 기반 L1 손실을 효과적으로 보완한다. 다양한 실험 결과, FreGS는 과잉 재구성을 완화하고 가우시안 밀집화 및 새로운 시점 합성 성능을 꾸준히 개선함을 확인할 수 있다(Fig. 1 참조).

 

 

Method

3.2 Frequency Regularization

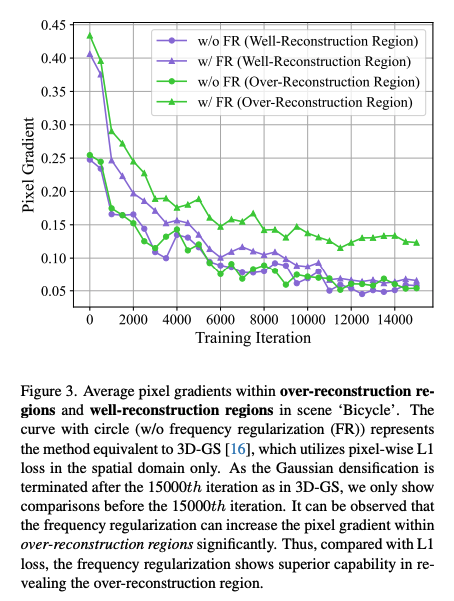
1. 과잉 재구성(Over-Reconstruction) 문제 (Fig. 3)

 

• 픽셀 기반 L1 손실만으로 학습 시, over-reconstruction 영역(고분산 영역이 소수의 큰 가우시안만으로 표현되는 구간)에서 평균 그래디언트가 작게 나타남.
• 이로 인해 해당 영역에 대한 가우시안 분할(split)을 유도하지 못해, 계속해서 큰 가우시안들이 남아 블러(blurring) 및 왜곡(artifacts)를 유발하게 됨.

 

2.  주파수 관점에서의 해결

• 주파수 공간은 서로 다른 주파수 성분(저주파, 고주파)을 명시적으로 분리하여 볼 수 있으므로, 블러나 세부 구조 손실 등을 더 직접적으로 파악 가능.
• 이 때문에, 주파수 영역에서 정규화(regularization)를 적용하면, over-reconstruction 영역에 대한 분할을 효과적으로 유도할 수 있음(평균 픽셀 그래디언트가 증가).
• 렌더링된 이미지와 실제 정답 이미지 각각에 대해 2D 이산 푸리에 변환(DFT)을 수행하여, 복소수 형태의 주파수 스펙트럼을 구함.
• 주파수의 진폭(amplitude)과 위상(phase)을 분리해 불일치를 측정하고, 그 차이를 손실로 정의하여 학습에 반영

 

수식

(2)  2D 이산 푸리에 변환

 

• $(x,y)$: 공간 도메인(이미지) 좌표
• $(u,v)$: 주파수 도메인 좌표
• $I(x,y)$: 실제 이미지에서의 픽셀 값
• $F(u,v)$: 복소수 형태의 주파수 값

(3, 4) 진폭과 위상

(5, 6) 진폭 및 위상 불일치

 

• $d_a$: 진폭 간 불일치 (Amplitude discrepancy)
• $d_p$​: 위상 간 불일치 (Phase discrepancy)
• $\hat{F}(u,v)$: 렌더링된 이미지 $\hat{I}$를 푸리에 변환한 값

 

3.3 Frequency Annealing 

 

1. 주파수 성분 분리 (저주파 / 고주파)

• 원본 푸리에 스펙트럼에 저역 통과 필터와 고역 통과 필터를 적용하여, 저주파 부분과 고주파 부분을 각각 분리한다.
• 저주파 성분은 전역(global) 구조나 대규모 특징을, 고주파 성분은 국소(local) 디테일이나 섬세한 엣지 정보를 주로 담는다.

2.  점진적 주파수 정규화(Progressive Frequency Regularization)

• 학습 초기에는 저주파 성분(LF)에 집중하여 전역 색감·구조를 먼저 맞추고,
• 학습이 진행됨에 따라 점차 고주파(HF)의 비중을 늘려, 디테일까지 정교하게 복원하도록 유도한다.
• 이를 위해, 학습 반복 𝑡에 따라 동적 고역 통과 필터 범위를 확장/조절하며, “주파수 어닐링(Frequency Annealing)”을 구현한다.

3.  손실 함수 

• 저주파/고주파 각각에 대해 진폭·위상(phase) 불일치를 계산한 뒤, 이를 가중합하여 최종 주파수 정규화 손실을 얻는다.
• 학습 초반에는 저주파만 사용하고, 후기에는 고주파 손실도 함께 고려한다.

수식

(7) 저주파 성분

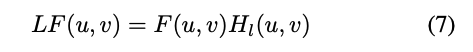
• $LF(u, v)$: 저주파(low-frequency) 성분
• $F(u, v)$: 원본(전체) 주파수 스펙트럼
• $H_l(u, v)$: 저역 통과(로우패스) 필터

(8) 고주파 성분

• $HF(u, v)$: 고주파(high-frequency) 성분
• $H_h(u, v)$: 고역 통과(하이패스) 필터

(9) 저주파 진폭 불일치 

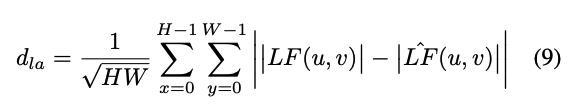
• $|LF(u,v)|$: 저주파 성분의 진폭
• $|LF_hat(u,v)|$: 렌더링된 이미지의 저주파 진폭
• $sqrt(H * W)$: 전체 주파수 성분 개수에 대한 정규화

(10) 저주파 진폭 불일치 

 

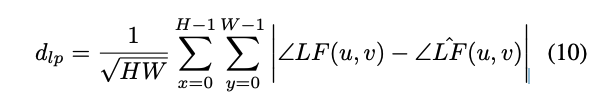
• $∠LF(u,v)$: 저주파 성분의 위상(phase)
• $∠LF_hat(u,v)$: 렌더링된 이미지의 저주파 위상

(11) 고주파 진폭 불일치 

 

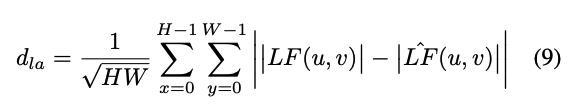
• $|HF(u,v)|$: 고주파 성분의 진폭
• $|HF_hat(u,v)|$: 렌더링된 이미지의 고주파 진폭

(12) 고주파 진폭 불일치 

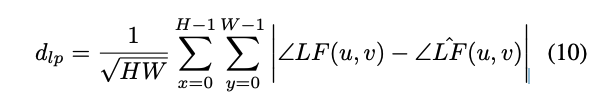
• $∠HF(u,v)$: 고주파 성분의 위상
• $∠HF_hat(u,v)$: 렌더링된 이미지의 고주파 위상

(12) 동적 고역통과 범위

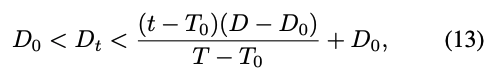
• $t$: 현재 학습 반복(iteration)
• $T_0$: 고주파 필터를 추가하기 시작하는 시점
• $T$: 전체 학습 반복의 최종 시점
• $D_0$: 초기 고주파 범위
• $D$: 최종 고주파 범위
• $D_t$: t 시점에서 동적으로 결정되는 고주파 허용 범위

(12) 최종 주파수 정규화 손실

• $L_f$: 최종 주파수 영역에서의 정규화 손실
• $w_l, w_h$: 각각 저주파, 고주파 정규화 항에 대한 가중치
• $(d_la, d_lp)$: 저주파 진폭·위상 불일치
• $(d_ha, d_hp)$: 고주파 진폭·위상 불일치
• $t$ 값이 $T_0$를 경계로 하여, 초반엔 저주파만 사용하다가 후반엔 고주파도 추가

 

 

 

Experiments

4.1 Datasets and Implementation Details

- Mip-NeRF360 데이터셋에 포함된 9개 장면 전부

- Tanks&Temples 데이터셋에 포함된 2개 장면

 

- L1 Loss + D-SSIM term

- 15,000 iteration 

- 초기에는 원본 이미지의 해상도보다 4배 낮은 해상도에서 학습을 시작하고, 500번의 반복 후 업샘플링(upsampling)을 통해 해상도를 원본 크기로 높임

- Adam 옵티마이저 

 

4.1 Comparisons with the State-of-the-Art 

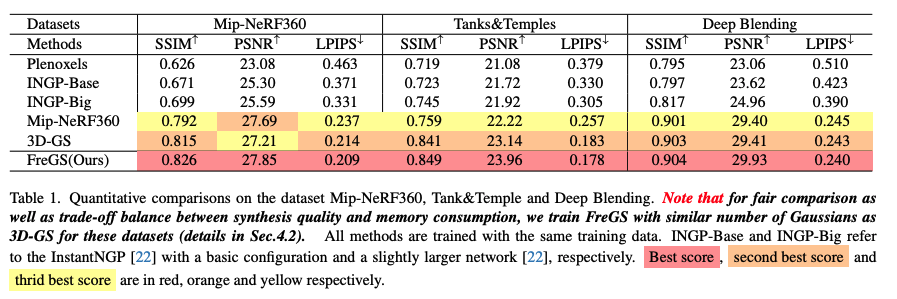
공정한 비교와 메모리·성능 간 균형 유지 차원에서, FreGS는 3D-GS와 유사한 가우시안 개수를 사용하도록 학습.

 

4.3 Ablation Studies 

Frequency Regularization과 Annealing을 적용한 Base+FR+FA 모델이 가우시안 스플래팅에서 PSNR, SSIM, LPIPS 지표를 크게 향상시켜 새로운 시점 합성에 중요한 역할을 함을 입증.

 

4.4 Visualizations

 

FreGS는 over-reconstruction 영역에서 더욱 많은 가우시안을 생성하고, 이를 통해 가우시안 밀집화를 명백히 개선하여 우수한 새로운 시점 합성 결과를 얻어낸다.  15,000번째 반복(iteration) 이후에는 가우시안 밀집화 과정이 종료되므로 가우시안 개수에 더 이상 변화가 없다.

 

 

---

Paper Link

https://arxiv.org/abs/2403.06908

FreGS: 3D Gaussian Splatting with Progressive Frequency Regularization

 

 

Google Scholar Link

https://scholar.google.co.kr/scholar?hl=ko&as_sdt=0%2C5&q=FreGS%3A+3D+Gaussian+Splatting+with+Progressive+Frequency+Regularization&btnG=

Google 학술 검색

 

 

GitHub

-